피보나치 수열은 다음처럼 정의된 수열이다(관련 내용은 [피보나치 돌 줍기 게임]참조).
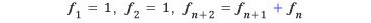
실제로 몇 항을 구해 보면 다음과 같다.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …
이 피보나치 수열은, 특히 황금비라 부르는 상수와 많은 관련이 있어 수학적으로 흥미롭다.

예루살렘 구시가에 있는 모스크, 바위사원. 황금비를 이루고 있다. <출처: (cc) Brian Jeffery Beggerly>
황금비란?
‘황금비’(golden ration)는 여러 가지 방법으로 정의할 수 있는데,
다음처럼 정의하는 것이 유클리드의 원론에 나오는 최초의 정의에 가깝다.
선분 AB의 길이를 x:1로 (단 x > 1) 내분한 점 C에 대해 AB:AC=AC:CB인 경우,
이런 분할을 황금분할이라 부르고 x를 황금비라 부른다.
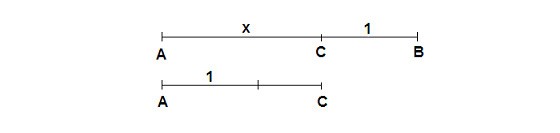
따라서 x+1 : x = x : 1이 성립하므로 x2 – x - 1=0이어야 한다.
왼편의 2차 다항식 x2 – x - 1은 피보나치 수열이나 황금비를 다루면 줄기차게 나오는 다항식이다.
아무튼 2차 방정식의 근의 공식으로부터 다음이 성립한다.
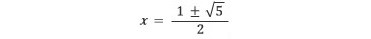
조건에서 x>1이라 하였으므로 황금비 ϕ (‘파이’(phi)라고 읽는다)는 아래와 같다.
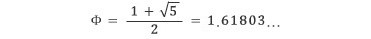
위의 방정식의 다른 근은 아래와 같은데,
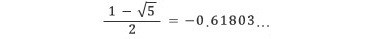
역시 알아둘 필요가 있다. 소수점 이하 자리수가 똑같다는 것도 관찰할 수 있는데,
이 값을 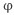 라 쓰기로 하자. (‘변형된 파이’라고 읽는다.)
라 쓰기로 하자. (‘변형된 파이’라고 읽는다.)
황금비의 연분수 전개와 피보나치 수
‘√2는 무리수’라는 글에서 연분수 얘기를 한 바 있으니,
잊어버렸거나 놓치신 분은 다시 한 번 읽어주시기 바란다.
황금비가 수학적으로 흥미로운 수라는 사실은 연분수 전개를 할 때도 드러난다.
ϕ=1.61803...의 정수부분이 1이므로 다음처럼 분해할 수 있다.
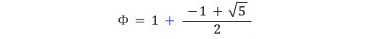
소수부분의 역수는 아래와 같으므로
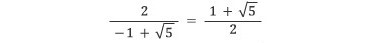
다시 (당연히) 황금비가 된다! 따라서 다음처럼 쓸 수 있다는 뜻이다.
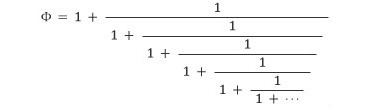
이제 이 연분수를 이용하여 황금비의 1단계, 2단계, 3단계, … 근삿값을 구해 보자. 즉
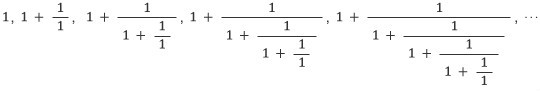
를 구하자는 뜻이다.
차례로 계산하면 1, 2/1, 3/2, 5/3, 8/5, 13/8, … 인데 분모 분자에서 피보나치 수열을 볼 수 있고,
서너 항만 계산해도 왜 피보나치 수열이 등장할 수밖에 없는지 쉽게 알 수 있다.
피보나치 수열의 일반항: 비네의 공식
방금 황금비의 연분수 전개에서,
피보나치 수열의 인접한 두 항의 비 fn+1 / fn가 황금비 ϕ로 수렴한다는 사실을 알았다.
피보나치 수열이 황금비와 관련돼 있다는 사실은 예를 들어 건축물 디자인 등에 암암리에 사용된다.
레오나르도 다빈치는 아름다운 인체의 비율을 표현하는데 황금비를 사용했다고 한다.
따라서 댄 브라운이 소설 ‘다빈치 코드’에 피보나치 수열을 등장시킨 것은 필연이라 하겠다.

다빈치의 자화상과 유명한 인체 드로잉인 비트루비안 맨(Vitruvian Man)
fn+1 / fn가 ϕ에 가까워진다는 관찰에서 fn+1 - ϕfn을 생각하기로 마음 먹으면,
피보나치 수열의 일반항을 구하는 공식을 얻는 데 한 걸음 가까워진다.
피보나치 수열을 구성하는 점화식
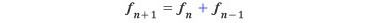
에, 근과 계수와의 관계 ϕ + 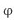 =1 및 ϕ
=1 및 ϕ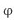 = -1 을 적용하면 다음을 알 수 있다.
= -1 을 적용하면 다음을 알 수 있다.
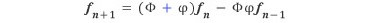
따라서 다음 두 사실을 얻는다.
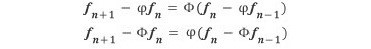
따라서
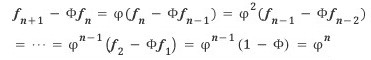
임을 알 수 있다. 마찬가지로 fn+1 - 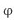 fn = ϕn도 성립한다.
fn = ϕn도 성립한다.
이 두 결과를 빼주고 정리하면, 선뜻 예상하기는 힘든 공식을 얻는다.
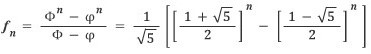
예를 들어 n=3을 대입하면
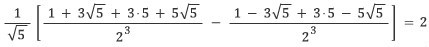
임을 확인할 수 있다.
방금 계산으로부터도 알 수 있지만
n이 큰 수일 때 실제로 공식에 대입해서 값을 구하는 게 만만한 일은 아니어서,
실제 항을 표현하는 자연수 값을 구하는 데 그다지 유용하지는 않다.
저 공식으로 다음처럼 f100을 구하느니, 차라리 차례대로 99번 더하는 게 낫다는 푸념도 나올 수 있다.
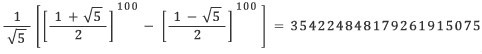
위 공식은 비네 (Jacques Philippe Marie Binnet, 1786-1856)의 이름을 따서 비네의 공식이라 부르는데,
저명한 수학자 겸 전산과학자 커누쓰(Donald Knuth)에 따르면
드 므아브르(Abraham De Moivre, 1667-1754)가 이미 알고 있었다고 한다.
그렇더라도, 피보나치 수열이 소개된 후 일반항 공식이 나오기까지 500년이나 걸렸다는 얘기인데,
공식의 모양을 보니 그럴 만도 했겠다.
황금비와 피보나치 수열의 관계
피보나치 수열의 이웃한 항의 비는 예를 들어
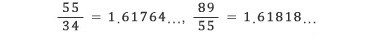
등은 황금비에 가까워지는 값이라고 했다.
더 정확하게는 n=1일 때만 제외하면, fnx ϕ에 가장 가까운 정수가 fn+1 이라는 사실도 알 수 있다. 예를 들어 10 번째 항 55에 황금비 1.61803…을 곱하면 88.9916…이므로 11 번째 피보나치 수는 89라는 얘기다. 이때도 n이 큰 경우 실제 계산에 이용하려면, 황금비의 정확한 근삿값을 알아야 한다는 단점이 있다.
한편 비네의 공식에서 아래 부분은
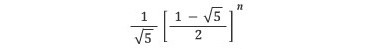
절댓값이 1/2보다 작으므로, fn은 ϕn / √5에 가장 가까운 정수라는 사실도 알 수 있다. 역시 n이 큰 경우 계산에 별 도움이 안 되기는 매한가지지만, fn의 자릿수를 아는 데 꽤나 유용하다. 상용로그를 아는 사람은, 예를 들어 100log(ϕ)-0.5log5가 20.54…라는 사실에서 f100이 21 자리수임을 알 수 있다.
피보나치 수열은 쓸데 없는 수열?
피보나치 수열은 흥미의 소재로만 다루어지는 경우가 많다. 그러다 보니, 쓸모라고는 찾아볼래야 찾아볼 수 없는 수열이라고만 여기는 경우가 많다. 또한 황금비와 관련하여 수학의 아름다움을 보여준답시고 억지 춘향처럼 꿰 맞춰 등장하는 경우가 많아, 오히려 진정한 가치는 외면되기 일쑤인 수열이다. 하지만, 특별한 이유도 없는 것 같으면서도 약방의 감초처럼 곳곳에서 불쑥불쑥 등장하는 수열이다.
이항 계수에 관련한 파스칼의 삼각형에 피보나치 수열이 등장한다는 것은 애교다. 주식 시장에서 주가 변동의 추세를 파악하는 방법론 중에서 황금비가 역할을 하는 경우도 있다. 드 므아브르는 피보나치 수열의 일반항을 연구하다 ‘생성함수’(generating function)를 발명하였는데, 이 개념이 수학에 미친 영향은 대단히 크다. 정수 계수 부정 방정식의 해를 찾는 알고리즘을 제시할 수 있느냐는 힐베르트의 10 번째 문제를 부정적으로 해결하는 데도 피보나치 수열이 중요하게 쓰였다. 두 정수의 최대공약수를 구하는 유클리드 호제법의 효율성에 관한 고찰에도 등장한다. 이 수열에 대한 박사 학위 논문도 있으며, 축구공 위의 수학자 강석진 교수의 논문에도 이 수열이 등장한다. 주로 이 수열과 관련한 수학만을 다루는 학술지도 있다. 흥미와 유용성을 동시에 갖춘 수열로는 단연 으뜸이라 하겠다.
'그리고 또 또, 또...' 카테고리의 다른 글
| 곧...나의 가족이 될 녀석들.... (0) | 2012.11.14 |
|---|---|
| 첫눈..... (0) | 2012.11.13 |
| 두 개의 직삼각형.....삼각자...... (0) | 2012.10.26 |
| 0...... (0) | 2012.10.16 |
| 아, 가을 , 귀뚜라미 (0) | 2012.09.07 |