수학시간에 사용하는 기구들은 매우 다양하지만, 쌍을 이루고 있는 기구로는 삼각자가 거의 유일하다. 초등학생들에게 삼각자는 ‘평면도형에 대해 학습할 때’, ‘각도 단원에서 측정을 학습할 때’, ‘수직과 평행 단원에서 두 직선의 수직과 평행을 학습할 때’ 등 다양한 수학학습을 위해 필수적인 교구이다. 또한 중학생들에게는 두 직선이 평행할 때 동위각과 엇각의 성질을 학습하는 단원에서 학습활동의 수단으로 사용되고 있다. 비록 고등학생이 되면 거의 사용하지는 않지만 삼각자에 대한 추억은 수학 속에 고스란히 남아 있는 것 같다. 이제 삼각자 속에 숨겨진 비밀을 구체적으로 살펴보기로 하자.
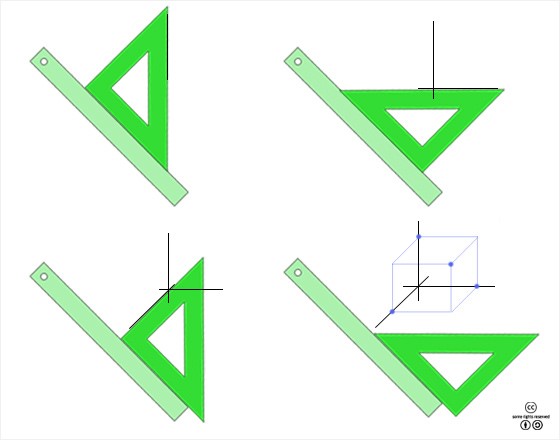
삼각자를 이용해서 정육면체의 투시도를 그리는 모습. 수직, 수평, 평행선 등, 삼각자의 용도를 잘 보여준다. <출처 : (cc) Dnu72 >
삼각자란?
삼각자에 대한 뜻을 국어 사전에서는 찾아보면,
‘삼각형으로 된 자,
보통 밑각이 60도, 30도로 된 직각삼각형과 두 밑각이 모두 45도로 된 직각이등변삼각형 두 가지가 있으며,
한 쪽 변에만 눈금이 있고 가운데에 구멍이 뚫려 있다’라고 정의하고 있다.
또한 영어사전에서는 삼각자를 ‘set square’ 혹은 ‘triangle’ 두 가지로 표현하고 있는데,
후자의 경우는 삼각형 모양이기 때문에 붙여진 것으로 보이고,
전자는 직각자(square)의 쌍이라는 의미로 붙여진 것 같다.
즉, 삼각자는 직각삼각형 모양의 자(ruler) 한 쌍을 가르킨다고 볼 수 있다.

삼각자와 직선 자
삼각자의 구성
그렇다면 삼각자는 처음부터 직각삼각형 모양의 자 한 쌍으로 구성되어 있었는가?
그렇지는 않은 것으로 보인다.
대표적인 예로
도메니코 페티(Domenico Fetti, 1588-1623)의 작품 ‘아르키메데스의 생각’이라는 그림(아래 왼쪽)과
독일의 한 건축물 외벽의 조각상(아래 오른쪽)을 보면 빗변이 없는 직각모양의 자 한 개만 볼 수 있다.

삼각자가 처음부터 직각삼각형 모양의 한 쌍의 자로 구성되지는 않았다
위의 그림과 사진에 나타난 삼각자를 보면,
삼각자가 선을 긋기에는 다소 불편한 모양을 가지고 있다.
사실, 삼각자는 선을 긋는 것보다 더 중요한 다른 기능이 가지고 있고,
그것은 삼각자의 구성과 매우 밀접한 관련이 있다.
정다각형을 이등분하여 합동인 직각삼각형을 얻을 수 있는 경우는 단 두 가지 경우 외에는 존재하지 않는다.
첫째는 정삼각형의 꼭짓점에서 대변에 내린 수선을 그으면, 합동인 두 직각삼각형으로 이등분하게 된다.
이 직각삼각형은 두 내각의 크기가 각각 30도, 60도인 직각삼각형이고, 오늘날 삼각자의 한 모양이 되었다.
둘째는 정사각형의 한 대각선을 그으면, 합동인 두 직각삼각형으로 이등분하게 된다.
이 직각삼각형은 한 내각의 크기가 45도인 직각삼각형이 되고, 오늘날 삼각자의 또 다른 한 모양이 된다.
따라서, 삼각자는 직각삼각형에서 일정한 각의 크기를 보장해 주고 있음을 알 수 있다.
즉, 30도, 45도, 60도, 90도의 각(이들 각을 특수각이라고 한다)을 정확하게 표현할 수 있는 역할을 하게 된다. 이를 통해 볼 때,
삼각자는 선을 긋는 것보다 특수각을 정확하게 그릴 수 있도록 고안된 수학기구로 볼 수 있다.
두 삼각자의 크기
이제 남은 것은 두 삼각자의 크기를 어떤 비율로 결정되어 있는가의 문제이다.
두 삼각자를 함께 보관하여야 하므로, 가능하면 두 삼각자의 크기(즉, 넓이)가 비슷해야 한다.
또 가능하면 긴 선을 그을 수 있으면 효율적이다.
이제 이 두 조건을 만족하는 것이 무엇인지 살펴보자.
삼각자의 보관의 편의를 위해서 두 직각삼각형의 한 변의 길이는 똑같이 맞추어져 있다.
두 직각삼각형에서 한 변의 길이를 똑같이 맞추는 경우의 수는 모두 여섯 가지 경우가 있다.
각각의 경우에 대해 살펴보자. 편의상 두 삼각자의 각 변의 이름을 아래와 같이 정해보자.
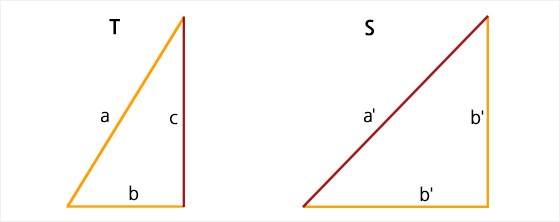
첫째, a=a’ 인 경우, (삼각형 T의 넓이) : (삼각형 S의 넓이) = √3 : 2가 된다.
둘째, a=b’인 경우, (삼각형 T의 넓이) : (삼각형 S의 넓이) = √3 : 4가 된다.
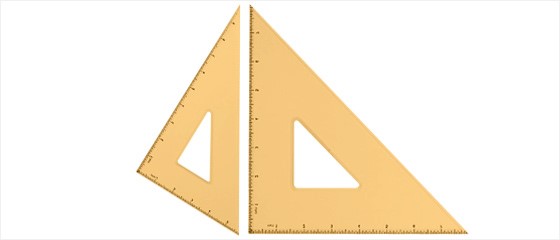
셋째, b=a’인 경우, (삼각형 T의 넓이) : (삼각형 S의 넓이) = 2√3 : 1이 된다.
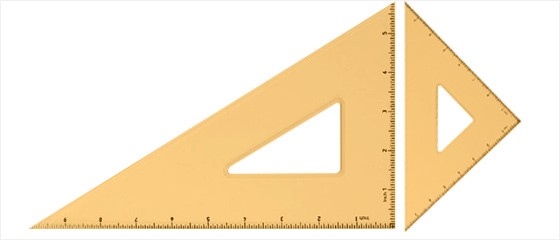
넷째, b=b’인 경우, (삼각형 T의 넓이) : (삼각형 S의 넓이) = √3 : 1이 된다.
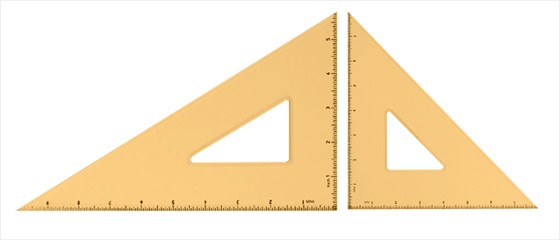
다섯째, c=a’인 경우, (삼각형 T의 넓이) : (삼각형 S의 넓이) = 2 : √3 이 된다.
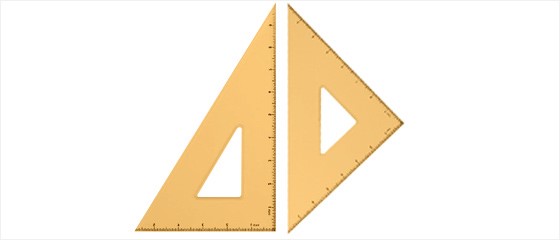
여섯째, c=b’인 경우, (삼각형 T의 넓이) : (삼각형 S의 넓이) = √3 : 3이 된다.
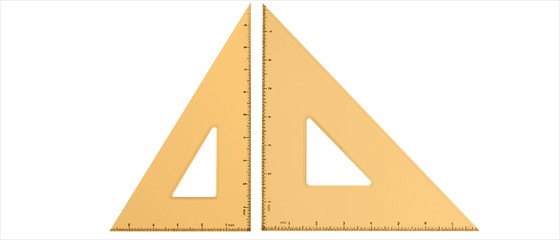
위 여섯 가지 경우 중에서 넓이의 차가 가장 작은 것은 첫째와 다섯째 경우이다.
사실 겉으로 보기에도 이 두 가지가 가장 안정된 모양을 가지고 있다.
그런데, 첫째 경우가 다섯째 경우보다 a의 변의 길이가 훨씬 짧기 때문에
최종적으로 다섯째 경우가 두 삼각자의 크기의 비로 결정된 것으로 보인다.
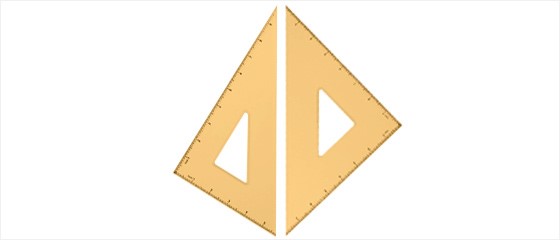
즉, 흔히 사용하는 삼각자는 아래와 같은 모양이 된 것이다.
두 삼각자가 동일한 점
앞에서처럼 두 삼각자를 T, S라고 하면,
삼각자 T의 빗변의 길이와 삼각자 S의 한 변의 길이는 서로 같다.
이것과 더불어 두 삼각자가 동일한 값을 가지는 것이 한 가지 더 있다. 그것이 무엇인지 살펴보자.
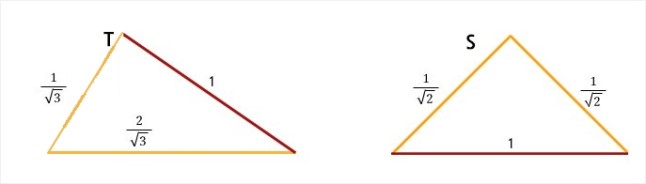
두 삼각자(T, S)의 빗변이 밑변이 되도록 위치시키고,
두 삼각형의 동일한 변의 길이를 1이라고 두면 각각의 변의 길이는 위 그림과 같아진다.
그러면, 삼각형 T의 높이 h와 삼각형 S의 높이 k는 모두 1/2로 같다.
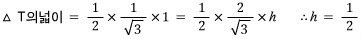
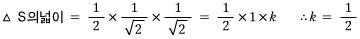
삼각자의 주 목적은 특수각
삼각자는 영어로 ‘set square’라고 불린다.
여기서 ‘square’는 직각자를 의미한다.
삼각자는 두 개로 구성되는데
그 이유는 정삼각형과 정사각형만이 이등분하여 직각삼각형을 얻을 수 있기 때문이다.
특별히 삼각자는 직선을 긋는 용도 보다는 특수각을 얻기 위해 고안된 것으로 보인다.
삼각자를 이용하면, 30도, 45도, 60도, 90도를 얻을 수 있기 때문에 모든 특수각을 정확하게 표현할 수 있다.
'그리고 또 또, 또...' 카테고리의 다른 글
| 첫눈..... (0) | 2012.11.13 |
|---|---|
| 피보나치 수열과 상관된...멋쟁이 상수...황금비.... (0) | 2012.10.26 |
| 0...... (0) | 2012.10.16 |
| 아, 가을 , 귀뚜라미 (0) | 2012.09.07 |
| 가을 (0) | 2012.09.04 |